THE CABLE MODEL - RANGE PREDICTION USING VEHICLE DEPTH AND CABLE LENGTH

When towing the sensor, the cable may assume a shape which can be described by the well known catenary formula ([9]).

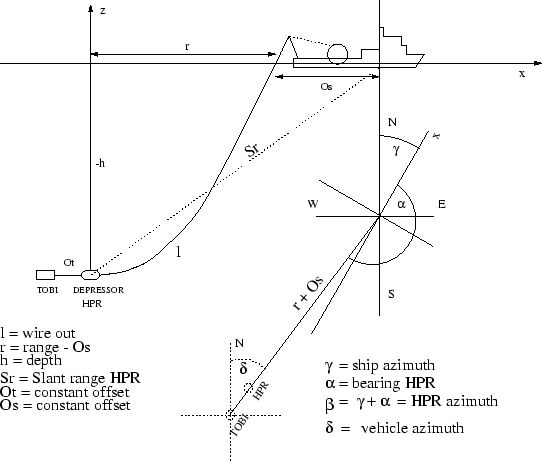
Herafter we will describe the procedure for calculating the best tow-fish position by the wire-out length and depth of the sensor.

In Fig.12 the analytical sketch of the problem is presented.

Figure 12: Analytical sketch of the tow-fish position problem. Note that the the catenary is schematic only and not to scale.Note also that acoustic variability and refraction of ray paths leads to errors in range (Sr) and depth derived by the Simrad HPR system.

The catenary equation can be written as:

$$z(x) = \frac{ah}{2} \Big[e^{x / h}+e^{-x / h}\Big] + b = ah \cosh \big(\frac{x}{h}\big) + b$$ (1)

where h is the vehicle depth, a and b are parameters to be determined according to the boundary conditions. We assume that:

$$\cases{ z(x)=-h & with $x=0$\ \cr z(x)=0 & with $x=r$\ \cr }$$ (2)

The cable length is :

$$l(r) = \int_0^r{\sqrt{1+{[z^\prime(x)]}^2}} dx$$ (3)

In order to obtain an analitycal expression of Eq.3, we approximate the function z(x) of Eq.1 by a 2^nd order Taylor expansion:

$${z}(x) \cong \tilde{z}(x) = z(0) + \frac{1}{2!} \frac{\parti... ...^2} \Bigg\vert_{x=0} x^2 = (ah+b) + \frac{1}{2}\frac{ax^2}{h}$$ (4)

Given the boundary conditions in (2) we obtain:

$$\cases{ a=\frac{2h^2}{r^2} \cr b=-h(1+\frac{2h^2}{r^2}) \cr} \Rightarrow \\ \tilde{z}(x) = \frac{h}{r^2}(x^2-r^2)$$ (5)

Given the Eq.3 the length of the cable is

$$l(r) = \int_0^r\sqrt{1+\Big[\frac{2hx}{r^2}\Big]^2}dx = \frac{2h}{r^2}\int_0^r\sqrt{\big(\frac{r^2}{2h}\big)^2+x^2} dx$$ (6)

Let $a=\frac{r^2}{2h}$, therefore Eq.6 becomes:

$$l(r) = \frac{1}{a} \int_0^r \sqrt{a^2+x^2}dx = \frac{1}{2} \Bigg\... ...r^2+4h^2} + \frac{r^2}{2h} \ln \Bigg[ \frac{2h+\sqrt{r^2+4h^2}}{r}\Bigg]\Bigg\}$$ (7)

Using Eq. 7 we are able to calculate the cable length given the range distance r and the vehicle depth h.

Given the cable length l₀ and vehicle depth h, in order to solve the inverse problem, we use the Newton-Rapson iterative method, that is:

f(r) = l(r)-l₀ = 0 (8)

The value of r can be obtained by:

$$r^{\jmath+1} = r^\jmath-\frac{f(r^\jmath)}{f^\prime(r^\jmath)}$$ (9)

where $\jmath$ indicates the $\jmath_{th}$ iteration, and

$$f^\prime(r) = \frac{r}{2} \Bigg\{\frac{1}{\sqrt{r^2+4h^2}} + \frac{1}{h} \ln \Bigg[\frac{2h+\sqrt{r^2+4h^2}}{r}\Bigg] +$$

$$\frac{1}{2h(2h+\sqrt{r^2+4h^2})} \Bigg[ \frac{r^2}{\sqrt{r^2+4h^2}} - 2h - \sqrt{r^2+4h^2} \Bigg]\Bigg\}$$ (10)

starting with the trial solution r⁽⁰⁾=h. The convergence of such aproximation to the desired solution r can be evaluated by the Banach's contraction mapping theorem:

the iteration is terminated when $\frac{\vert r^{j+1} - r^j\vert}{r^{j+1}}$ is sufficiently small.