Optical properties measurements

The optical properties of coastal waters IOCCG2000, MOBLEY2004 can present wide spatial and seasonal variations related to the delivery of pigmented materials from surrounding watersheds and under the influence of the open sea water. Various dissolved and suspended substances (organic and inorganic) interacting with light along the water column influence in-water optical properties: these substances are defined as Optically Active Constituents (OAC), such as Tripton, Colored Dissolved Organic Matter (CDOM) and Chlorophyll (Chl). Their composition, concentration and size directly influence the Inherent Optical Properties (IOPs) of the water column, defined as the light absorption a($\lambda$), scattering b($\lambda$), backscattering bb($\lambda$) and attenuation c($\lambda$) coefficients. This set of properties constitutes the bio-optical model and allows us to determine the relations between the water constituents concentrations and the reflectance acquired above the water surface. Exploration of the relationship between the specific IOPs regional and temporal variability and biogeochemical quantities in coastal waters is essential for the modelling of underwater light field and represents distinct challenges for future regional remote sensing algorithms development. The Remote Sensing Reflectance (Rrs) spectrum is a result of the cumulative interactions of light with the water itself and the water quality parameters. To retrieve the water quality parameter concentrations, it is necessary to invert the reflectance spectrum. The water quality parameter concentrations and the reflectance spectrum are linked by the IOPs of the water. Any successful semi-analytic inversion approach needs to relate the water leaving reflectance to the IOPs, and then the IOPs to the water quality parameter concentrations. The IOPs and water quality parameter concentration relationship can be established by normalising the IOPs by the relevant water quality parameter concentration to calculate the specific inherent optical properties (SIOPs). The in situ measurements allow defining a different set of SIOPs for each sampling station. By means of the Hydrolight software, the Remote Sensing Reflectance (Rrs) is simulated considering all the parameters recorded at the time of the sampling (water constituents concentrations, illumination and acquisition geometry, wind speed, absorption and scattering coefficients). Comparing the simulated Rrs with the Rrs collected in situ it will be possible to verify the suitability of the adopted models and of the simulation procedures.

The radiometric in situ measurements were performed to achieve a comprehensive dataset of OACs concentrations and of SIOPs, leading to the parameterization of a three-component bio-optical model (Chl, CDOM, tripton). At all stations, discrete water samples for absorption and concentration measurements were collected from the surface. Filtration was performed immediately after sampling. Filters were kept in liquid nitrogen and then stored at -80until analysis; all protocols described below are compliant with those recommended for SeaWIFS calibration/validation activities. Different illumination conditions were encountered during the fieldwork: clear, cloudy and covered skies. During partly cloudy conditions, the measurements were not carried out. The sea surface was quasi-plane and the wind speed lower than 5 m/s. The calibration and validation of satellite and/or airborne ocean remote sensing data requires field Rrs measurements concurrently with the collection of water samples. Water-leaving reflectance Rrs was calculated from above-water measurements using a Photo Research-Spectrascan PR-650 field portable hyperspectral radiometer operating between 380 and 780 nm with 4 nm resolution. The Rrs signal (in sr$^{-1}$) is calculated from:

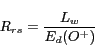$$R_{rs} = \frac { L_w }{E_d(O^+) }$$ (1)

where L$_w$ (W m$^{-2}$ sr$^{-1}$ nm$^{-1}$) is the water-leaving radiance and E$_d$(O$^+$) (W m$^{-2}$ sr$^{-1}$ nm$^{-1}$) is the downwelling irradiance incident on the water surface. The wavelength dependance of the parameters is omitted to simplify the notation. L$_w$ also depends on the viewing direction, defined by the zenith and azimuth angles I$_z$ and I$_a$. Ed(0+) can be measured above the water surface, directly using an irradiance sensor, or using a radiance sensor and a reference plaque of a known reflectance. L$_w$ cannot be directly measured and it is determined from above-water or in-water measurements. In each station, the upwelling radiance L$_u$ and the sky radiance L$_{sky}$ were successively measured above the water surface (5 couples of measures) with an oblique viewing, respectively $\Theta$=40°, $\phi$=90°and $\Theta$=130°, $\phi$=90°. The upwelling radiance L$_u$ can be expressed as

$$L_u = L_w + L_r$$ (2)

where L$_r$ is the radiance signal resulting from reflection effects at the air/water interface, namely the sun and sky glint. L$_r$ is due to a certain percentage ($\rho$) of the sky radiance L$_{sky}$ reflected at the surface. The percentage $\rho$ is the reflection coefficient for the wave-roughened air-water interface: it is a complex factor that depends on incident light and viewing directions, wavelength and wind speed. It also depends on the sensor field-of-view and sky radiance distribution.