MODELING OF WAVE PROPAGATION

The loss of energy of the wave front in water is due to (a) geometrical spreding, proportional to distance from source, (b) absorption due to medium viscosity, proportional to frequecy squared, and (c) molecular relaxation induced by sound wave pressure. We used an algorithm based on parabolic equation that handles efficiently 'Range Dependent' ocean acoustic propagation problems [Collins (1999)].

The propagator is determined by

$$\frac{\vartheta^2 p}{\vartheta r^2} + \rho \frac{\vartheta}... ... \frac{1}{\rho} \frac{\vartheta p}{\vartheta z} ) + k^2 p = 0$$ (1)

where $\rho$ is density, $k=(1+i\eta \beta)\omega / c$ wave number, $\omega$ angular frequency, $c$ speed of sound in water, $\beta$ attenuation (dB/Km), $\eta=(40\pi log(e))^{-1}$.

By solving, we obtain

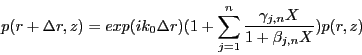$$p(r+\Delta r,z) = exp(ik_0\Delta r) ( 1+\sum_{j=1}^{n} \frac{\gamma_{j,n} X}{1+\beta_{j,n} X} ) p(r,z)$$ (2)

pressure variation between $r$ and $(\Delta r,z)$, where $z$ is depth.